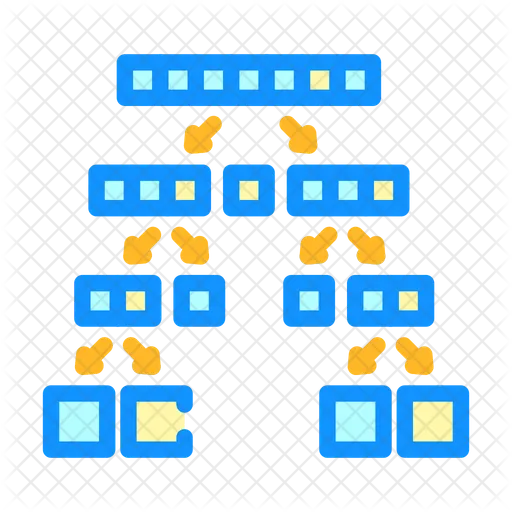
How does quick sort work step by step?

Quick sort picks a pivot element, then partitions the array so all elements smaller than the pivot come before it and all larger elements come after. It then recursively quick sorts the two partitions until the whole array is sorted.

What is the time complexity of quick sort?

Quick sort has O(n log n) average and best-case time complexity, but degrades to O(n²) in the worst case when a poor pivot is chosen (e.g., repeatedly picking the smallest or largest element). Randomizing the pivot avoids this in practice.

Is quick sort stable?

No. The standard in-place quick sort is NOT stable, because partitioning swaps elements non-adjacently, which can reorder equal keys.

Quick Sort

Normal

L R

How to use ?

Enter an array separated by commas as : 16,15,15,10,1 or just press the hand icon to generate a random array then press enter or Sort button. Sorting will start and you can watch each pass as it gets sorted. When it shows green it means the two of them are being compared when red shows, it means the left number is greater than right number so it needs swapping The blue color means the number is at its correct position and thus sorted it will continue to check other numbers until it reaches end.

Quick Sort Overview

History

Quick sort was developed by Tony Hoare in 1960. It is a divide-and-conquer algorithm that is efficient for large datasets. Quick sort has become one of the most widely used sorting algorithms due to its performance in practice and its ability to sort in place.

Current Uses

General Purpose: Used in a variety of applications, including databases and memory sorting.
Libraries: Often implemented in standard libraries for programming languages due to its efficiency.
Embedded Systems: Commonly used in systems with limited resources for efficient sorting.

Time and Space Complexity

Time Complexity

Best Case: O(n log n) - When the pivot divides the array into nearly equal halves.
Average Case: O(n log n) - The average case performance is efficient.
Worst Case: O(n²) - Occurs when the smallest or largest element is always chosen as the pivot.

Space Complexity

Space Complexity: O(log n) - Due to the recursive stack space used during the algorithm's execution.

Pseudo Code

function quickSort(arr, low, high):
    if low < high:
        pi = partition(arr, low, high)
        quickSort(arr, low, pi - 1)
        quickSort(arr, pi + 1, high)

function partition(arr, low, high):
    pivot = arr[high]
    i = low - 1
    for j from low to high - 1:
        if arr[j] <= pivot:
            i = i + 1
            swap arr[i] and arr[j]
    swap arr[i + 1] and arr[high]
    return i + 1

Key Characteristics

In-Place: Quick sort requires minimal additional storage space.
Not Stable: The algorithm is not stable due to the way it swaps elements.

Summary

Quick sort is a highly efficient sorting algorithm that utilizes the divide-and-conquer strategy. Despite its worst-case time complexity of O(n²), it is widely used due to its average-case efficiency and practical performance.

How Quick Sort Works

Quick sort is a divide-and-conquer algorithm built around the idea of a pivot. Its efficiency comes from partitioning the array in place:

Choose a pivot element (any element - often the last, first, or a random one).
Partition the array so that every element smaller than the pivot comes before it, and every element larger comes after it. The pivot is now in its final sorted position.
Recursively quick sort the sub-array to the left of the pivot and the sub-array to the right.
Terminate when a sub-array has zero or one element - the whole array is then sorted.

On average quick sort makes O(n log n) comparisons and is famously cache-friendly, which is why it is so fast in practice - but its worst case is O(n²) when the pivot is consistently the smallest or largest element (randomizing the pivot avoids this).

When To Use Quick Sort

Random or shuffled data: excellent expected performance with low overhead.
Average-case sensitive workloads: cache-friendly partitioning beats merge sort in most comparisons.
In-place sorting: uses only O(log n) stack space.
Base of Introsort: combined with heap and insertion sort for production C++ std::sort.

Quick Sort Code Implementation